Галактический Ковчег

Музыка небесных сфер

Шахерезада

Дата: Четверг, 2023-02-09, 4:47 PM | Сообщение # 21

Хранитель Ковчега

Группа: Проверенные

Сообщений: 3891

Статус: Offline

...продолжение -
Вальтер Буркерт 83

4. ГАРМОНИЯ СФЕР И АСТРАЛЬНОЕ БЕССМЕРТИЕ

88 Астрономия и пифагореизм

привлекается,272 но Платон явно говорит, что движение мировой души происходит ᾄνευ φθόγγου καὶ ἠχῆς (37b); мифический образ Сирен из «Государства» переносится в мир нематериального и абстрактного. В то же время отвергается наивное представление пифагорейцев, которые, согласно Аристотелю,273 думали, что огромные тела звезд не могут двигаться без шума. В «Государстве», в открытой полемике против пифагорейцев, Платон требует, чтобы гармония чисел рассматривалась сама по себе, без всякой отсылки к слышимым звукам, и сам проводит эту программу в «Тимее».274 Таким образом, отношение между астрономией и музыкой доводится до предельного, нематериального принципа. Все
числа по порядку являются первоначалами космоса, который в то же самое время есть «красота» и отражение «Блага». Тем не менее, основные составляющие материи, элементы, также происходят из процесса геометрического упорядочивания. Все это, как показывают тексты Аристотеля и Платона, не пифагорейское, а платоническое.

272 Это было отвергнуто Rivaud, Rev. hist, philos. 3 (1929) 16ff (он посчитал
необходимым заклеймить как пост-платоновские подделки не только
фрагменты Филолая, но и фрагменты Архита; он, похоже, не заметил, на стр. 6f,
что сам Платон в «Государстве» 530, явно говорит о пифагорейской
музыкальной теории). Гармония сфер, как он полагает, просто грубая
интерпретация «Тимея». (Похоже рассуждает Moreau, Âme 55.)
273 «О небе» 290b15.
274 «Государство» 531c; ср. ниже, гл. V 1.

Вальтер Буркерт 89

Противоречивая природа поздней традиции, где иногда используются семь,275 иногда восемь,276 а иногда и три музыкальные ноты,277 и в которой девять муз ассоциируются со сферой Всего,278 показывает, что идея космической музыки не связана с какой-либо отдельной астрономической системой. Этот концепт не связан с математической или музыкальной теорией, но имеет более глубокие корни; и это то, что позволило ему пережить даже Птолемееву космологию. Это, конечно же, подразумевает, что любое заключение о каких-либо астрономических теориях пифагорейцев на основе гармонии сфер, опасно в принципе. Не следует предполагать, что в их основе лежит какая-то детальная система. Есть и другие концепции космической музыки, довольно отличающиеся, но все же имеющие отношение друг другу. Совсем не обязательно говорить о планетах, или многоэтажной вселенной. Не важно,
как разделены вещи, правильно настроенное ухо все равно услышит музыку.279 У древней лиры было только четыре струны, «имитирующих космическую музыку, которая состоит из четырех элементов».280 В свою очередь, четыре сезона соответствуют элементам и находятся в согласии

275 Выше, сн. 7. Также прослеживалась связь с 7-ю гласными: Nicom. Exc. 6 p.
276 Jan; Schol. Dion. Thr. p. 197.33ff Hilgart; гностик Марк ap. Hippol. Ref. 6.48;
Nicom. Th. ar. 71.13ff; Lydus Mens. 2.3; CIG II1 no. 2895; cf. F. Dornseiff, Das
Alphabet in Mystik und Magie (Leipzig, 19252
) 82f.
276 Платон и Эратосфен, выше, сн. 12. Аритмологический источник (Theo
Sm., Anatolius) ассоциирует музыку сфер с пассажем из Эратосфена в их
дискуссии о числе восемь, а не семь.
277 В λόγος дельфийцев (Plut. Quaest. сопv. 745a.) Burnet (EGP 110) и Kranz
(Philologus 1938, 437) усматривали указание на то, что Пифагор ассоциировал 3
«кольца» Анаксимандра (звезды, Луна и Солнце) с основными интервалами кварта,
квинта и октава.
278 Восьмая муза Урания вполне подходит; а девятой была либо concinentia
maxima – Каллиопа, как προφερεστάτη ἁπασέων (Macrob. Somn. Sc. 2.3.1f) – либо
относилась к «региону земли» (Plut. De an. Procr. 32.1029d, Quaest. conv. 746a).
Другие обращались за помощью к идее о Противо-земле (Por. VP 31).
279 Можно упомянуть ассоциацию астрологических конфигураций с
музыкальными аккордами (Plut. De an. Procr. 31.1028d-e, Ptol. Harm. 3.9).
Птолемей в «Гармонике» (Harm. 3) представляет хороший пример таких
искусных выходок. Ср. также Phld. Mus. p. 100 Kemke.
280 Boeth. Mus. 1.20 p. 206 Friedlein, из Nicomachus. Ср. Clem. Al. Protr. 1.5.1:
огонь как νήτη.

90 Астрономия и пифагореизм

друг с другом: весна с осенью составляют кварту, с зимой – квинту, с
летом – октаву, «так, как они говорят, считал Пифагор».281 Все источники на эту тему поздние, а часть об элементах сознательно заимствована из «Тимея».282 Но Скифин и Клеанф называют Солнце «плектром (медиатором)» космоса, что гораздо лучше подходит для объяснения ритма сезонов, который действительно зависит от положения Солнца, нежели для объяснения планетарной иерархии.283 О гармонии (ἁρμονία) сезонов говорится у Еврипида, а затем и у Платона.284 Такие идеи восходят к восточным истокам.285 Идея космической музыки, особенно связанной со сменой времен года, распространена довольно широко:

281 Aristid. Quint. 3, p. 144f M.: лето это 4, осень 6, зима 12, весна 8; также Plut.
De an. procr. 31.1028f («Халдеи»); несколько иначе в Hymn. Orph. 34.10ff (зима это
Гипата, лето – Нета, весна – дорический тон: Меса?); единственный намек,
Hymn. Orph. 8.9. O. Neugebauer, AJP 63 (1942) 455–488, ошибочно пытается
извлечь точный астрономический смысл из пассажа Плутарха и представить
действительные различия астрономических сезонов в качестве гармонических
чисел. Он упускает из виду объяснение у Аристида и, кроме того, вынужден
предположить смешение осени и лета. Кроме того, любое подобное рассуждение
основано на контрасте лета и зимы.
282 Aristid. Quint. 3, pp. 144f M. Платон говорит об ἀναλογία как о δεσμός
элементов («Тимей» 31b–c), и выводит из этого тот факт, что их четыре; таким
образом, он знает о некоторого рода «гармонии элементов»; но правильные тела
(polyhedra) не могут быть связаны с этим напрямую. Платон интересуется не
точным и правильным расчетом, но намеками по поводу базовой структурой
реальности.
283 Выше, гл. IV 1, сн. 107.
284 Еврипид, фр. 943 (Лобек (Lobeck) считает его сомнительным), Платон
«Пир» 188a, «Филеб» 26a, где Платон, кажется, обсуждает пифагорейские темы.
285 Плутарх (Plut. De an. procr. 31) говорит о «халдеях». Диодор сообщает, о
Гермесе-Тоте: λύραν τε εὑρεῖν, ἣν ποιῆσαι (чтение Буркерта: λύραν τε νευρίνην
ποιῆσαι) τρίχορδον μιμησάμενον τὰς κατ' ἐνιαυτὸν ὥρας· τρεῖς γὰρ αὐτὸν
ὑποστήσασθαι φθόγγους, ὀξὺν καὶ βαρὺν καὶ μέσον, ὀξὺν μὲν ἀπὸ τοῦ θέρους, βαρὺν
δὲ ἀπὸ τοῦ χειμῶνος, μέσον δὲ ἀπὸ τοῦ ἔαρος (1.16.1; Hecataeus of Abdera, FGrHist
264F25 [?]; ср. W. Spoerri, Späthellenistische Berichte über Welt, Kultur und Götter
[Basel, 1959] 164ff). Когда Эратосфен в своем «Гермесе» представлял бога в
качестве изобретателя гармонии сфер, он, очевидно, объединял египетские
элементы с греко-пифагорейским материалом. Келлер (G. A. Keller, Eratosthenes
und die alexandrinische Sterndichtung [Diss. Zurich, 1946] 95ff, 98ff) решительно
отрицает какое-либо египетское влияние на Эратосфена. Но трех-струнная лира

Вальтер Буркерт 91

например, пять нот китайской музыки соответствуют пяти элементам и сезонам.286 Здесь не следует предполагать прямого влияния, скорее следует говорить о параллельном развитии в силу схожих психологических импульсов. И именно в этом могут выявиться корни идеи космической музыки, а не в контексте планетарной иерархии. До начала рефлексивного мышления, человек, в различных контекстах, испытывает влияния. Он неосознанно помещает множество явлений в ограниченное число схем. А лишь оформившийся рефлексивный подход далее выводит эти переходные прозрения в область сознания, именует их и связывает друг с другом. Так постигается мир. В мифе и ритуале человек также пытается сделать эти явления наличными и явными, убеждает себя в том, что, несмотря на все затруднения и всевозможные окружающие его опасности, все находится «в порядке».
Именно в такой донаучной концепции порядка возникает идея космической музыки, и числовые спекуляции вырастают на этой же почве. Но взаимосвязи, оказывающие свой эффект обычно бессознательно, или проникающие в сознание лишь в качестве результата медленной и
настойчивой рефлексии, в состоянии экстаза становятся непосредственным и ошеломляющим опытом. Душа в экстазе, во сне или в трансе путешествует на небеса, слышит там музыку космоса, чьи мистические структуры сразу же становятся ей понятными. Несравненный и
сверхъестественный звук, наряду с несравненной красотой и яркостью иных миров, является частью одного целого.287 Если Пифагор был кем-то вроде шамана, который в экстазе имел контакт с потусторонним миром, тогда традиция, утверждающая, что он лично слышал небесную музыку, сохранила долю истины.288 Взглянув за фасад анализа и объяснения гармонии сфер, мы находим там не эмпирическую и не

египетская (Keller, 99). Гермес, как изобретатель лиры, является греком, а Тот,
как изобретатель астрономии, египтянин (Платон «Федр» 274c).
286 См. E. M. von Hornbostel, "Tonart und Ethos," Festschr. J.Wolf (Berlin, 1929),
я не могу проверить предположение Хорнбостела о похожих идеях у арабов. О
китайцах см. M. Granet, La pensée chinoise (Paris, 1934) 209ff.
287 Гл. IV 3, сн. 50.
288 Выше, сн. 3. Ср. также Платон «Государство» 617b, Nechepso–Petosiris fr. 1
Riese = Vett. Val. 6 prooem. p. 241 Kroll: ἔδοξε δέ μοι πάννυχον πρὸς ἀέρα...καί μοί
τις ἐξήχησεν οὐρανοῦ βοή; Cic. Rep. 6.18, Plut. De gen. 590c, De fac. 944ab, Corp.
Herm. 1.25.
92 Астрономия и пифагореизм

математическую науку, но эсхатологию. В религии Заратустры рай, к которому восходит душа, называется гародемана – «Дом Псалмов». К Пифагору это имеет отношение в том смысле, что в свой смертный час он
попросил, чтобы играл монохорд: «Души не могут восходить без музыки».289
Неоднократно внимание уделялось тому немаловажному факту, что
изменения греческих представлений о судьбе умершего происходили
под влиянием развития астрономических познаний.290 Если мы знаем,
что Земля сферична, повсюду населена и ограничена в размере, для подземного Аида Гомера или для «Островов блаженных» на далеком Западе
просто не остается места. В основном доминировала идея о том, что Потусторонний мир находится в области звезд, и что человеческая душа
приходит с небес и в определенный день туда же вернется. Такие представления со многими вариациями в деталях доминировали с конца эллинистического периода, как в литературных работах, так и в искусстве
и надгробных надписях.291 Современные исследователи, следуя античной традиции в поисках решающего поворотного момента в этом развитии увидели восточные влияния – вавилонское и иранское – и, что примечательно, влияние пифагореизма.292
289 Aristid. Quint. 3, p. 116 M. = p. 97 W.–I.; Варрон о лире Орфея в схолиях к
Вергилию (изд. J. J. Savage, ТАРА 56 (1925) 235); ср. A. D. Nock, CR 41 (1927) 169–
171, 43 (1929) 60.
290 Часто отмечается у Кюмона (Cumont, After–life 91ff, Or. rel. 114ff, 270f,
Symb. passim, Lux esp. 142ff). См. также Capelle; Pfeiffer, Sterngl. 113ff; Carcopino,
Bas. 266ff; Nilsson II 470ff, Op. III 250–265; van der Waerden, Anf. 204–252.
291 Ср. в особенности Cic Somn. Sc, утраченный трактат Consolatio, и Hort. fr.
97 Müller; Vergil Aen. 6 (with Norden, Vеrgil VI, 23ff); Plut. De sera 563ff, De gen.
589ff, De fac. 942ff. Надгробные надписи собраны Capelle 33ff; Rougier 108 n. 1; R.
Lattimore, Themes in Greek and Latin Epitaphs (1942) 31–43; P. Lambrechts, Hommages Déonna (Brussels, 1957) 322ff. Ни одна полностью не сохранилась.
О символизме надгробий, Cumont, Symb. passim; об изображении восхождения
и нисхождения души в митраизме, Cumont, Or. rel. 114ff, 145f, 290 n. 69. –
О возможной роли Посидония в этом отношении, см. Reinhardt, Kosmos 276ff,
308ff, RE XXII 778–791.
292 Кюмон видит источник в слиянии вавилонской астральной религии с
персидским дуализмом (After-Life 95, Or. rel. 272 n. 91, Symb. 264, Lux 143ff). См.
также Pfeiffer, Sterngl. 113ff. Bidez, Eos 9ff, 98f, считает, что источник был
вавилонский, но идея передавалась через пифагорейцев, ван дер Варден думает

Сказки - жемчуга мира
Книги Семи Морей

Шахерезада

Дата: Четверг, 2023-02-09, 4:47 PM | Сообщение # 22

Хранитель Ковчега

Группа: Проверенные

Сообщений: 3891

Статус: Offline

Вальтер Буркерт 93

Ружье (Rougier) попытался представить веру в то, что мир бессмертных находится среди звезд, как дедукцию из астрономического открытия
Пифагора, делая, таким образом, религиозную идею логическим заключением из научного знания, что не убедительно с точки зрения истории как
религии, так и астрономии.293 Думать, что за «гомеровской религией» по-

так же. Вместе с Ружье (Rougier), Буаянсе (Boyancé, REG 1952, 314f)
предостерегает от поспешного вывода о восточном происхождении, однако
настаивает на роли пифагорейцев и даже самого Пифагора (349), но также и на
роли древнейших верований и позже платонизма. Нильсон (Nilsson, Op. III
250ff) занимает похожую позицию.
293 Согласно Ружье (Rougier), источник этой идеи не в религиозных
фантазиях жителей Востока, но в революционной астрономии Пифагора ("la révolution astronomiquе dе Pythagorе" (21ff)), то есть в открытии математической
физики. Открытие Пифагором движения Солнца через зодиак в другом
направлении означало, что движение одной из так называемых планет
наблюдалось как идеально круговое, и признавался математический порядок
небесных явлений. В качестве «conséquences religieuses» (42ff) из этого
возникают доктрины о присутствии душ на звездах и об их божественности, об
отношении между звездой и душой, из-за их вечного движения, дуализма
небесного порядка и земного беспорядка; и, как считает Ружье, отражения этих
доктрин у Алкмеона подтверждают, что их автором был Пифагор. На это можно
ответить, во-первых, что для простого наблюдателя Солнце является не
планетой, а парадигмой космического порядка (выше, гл. IV 2, сн. 18). Его
движение по зодиаку уже было известно Клеострату, не говоря о вавилонянах,
и понятие независимого движения планет древнее ионийской вихревой теории
(выше, гл. IV 2). В таком случае, во всем этом не было такого открытия, которое
должно было означать «астрономическую революцию». Ружье правильно
сделал, что вовремя перестал приписывать пифагорейцам математическую
теорию действительных движений планет. Он признает авторство Евдокса
(26ff) и не вводит теорию эпициклов в дискуссию, хотя он действительно
выдвинул смутное предположение, что пифагорейцы могли применять
объяснение такого же рода, как и для Солнца к другим планетам (22); но здесь
он перестает замечать, что тот пассаж из Теона, который он цитирует (150,12ff),
вводит анахронистические эпициклы. Ружье пропускает важную часть
свидетельства, акусму о планетах как «псах Персефоны», которая действительно
обуславливает связь между пифагорейским учением и восточными идеями, кои,
с его точки зрения, радикально отличаются (выше, гл. IV 1, сн. 109). В качестве
аргумента против Ружье, см. также Cumont, Symb. 116 n. 3, Lux 147 n. 1. – В 1959

94 Астрономия и пифагореизм

следовала «пифагорейская революция» – это довольно опасное упрощение. В народных верованиях о загробной жизни испокон веков было представлено великое множество схожих и противоположных тем; 294 даже у Гомера идея затхлого «дома Аида», ненавистного богам, сосуществовала с «Полями блаженных» и культом обожествления Геракла. 295 Мистериальные культы приносят человеку веру в то, что можно избежать смерти и встретиться с богами; и от этой доктрины остается один простой шаг к представлению о том, что человек сам имеет божественное происхождение и после смерти вернется к своим истокам.296 Ассоциация богов с
небесами имеет первобытное происхождение и, в принципе, выглядит довольно очевидной.297 Уже в архаический период известны изображения путешествия обожествленного умершего в потусторонний мир. Табун крылатых лошадей обеспечивает эскорт на «небеса»,298 тогда как морские создания – тритоны, нереиды, дельфины – указывают путь к

году Ружье переиздал свою работу 1933 года практически без изменений (La religion astrale des Pythagoriciens), но не включил ссылки, так что следует цитировать более раннюю работу.
294 Маори могут изображать нисхождение мертвых в подземный мир, утверждая в тоже время, что они живут на десятом небе, говорит Леви-Брюль (L. Lévy-Bruhl, The "Soul" of the Primitive 175). Так, участвуя в ритуале Трофония, Тимарх путешествует в недра и благодаря этому переносится на звезды (Plut. De gen. 22.590b; ср. Vergil Aen. 6, и ниже, сн. 46).
295 Сама идея «Полей блаженных» демонстрирует соединение почитания
молнии и мифа об «Островах блаженных» (Burkert, Glotta 39 [1961] 208ff).
Обожествление Геракла – это, несомненно, очень старый миф, хотя
посвященные этому строки в «Одиссее» (Od. 11.601ff) и у Гесиода (фр. 25.26-33
M.-W.) объявлялись в античности недействительными (athetized).
296 О τὸν λοιπὸν χρόνον μετὰ θεῶν διάγειν, как о цели мистериальных культов,
см. Платон «Федр» 81 a. Так же золотые пластинки: θεός ἐγένου ἐξ ἀνθρώπου (DK
1 B18, 20) и καὶ γὰρ ἐγὼν ὑμῶν γένος ὄλβιον εὔχομαι εἶναι (DK 1 В18.3, 19.3; ср. 17.7,
17.6, I7a3).
297 θεοὶ οὐρανίωνες, ср. взаимосвязь корня и идеи Zeus, deus, dies. Об Олимпе,
выше, гл. III 2, сн. 31. Дионис тоже связан со звездами: ἰὼ πῦρ πνεόντων χόραγ᾽
ἄστρων, Soph. Ant. 1147; ср. Diod. 1.11: Εὔμολπος μὲν ἐν τοῖς βακχικοῖς ἔπεσί φησιν.
ἀστροφαῆ Διόνυσον ἐν ἀκτίνεσσι πυρωπόν. Мусей, отец Евмолпа, – это сын
Селены (выше, гл. IV 3, сн. 48).
298 Этрусские геммы (Furtwängler, Gemmen I pl. 7, nos. 1, 2, 3, ca. 600 B.C.)
сравнивались с мифом из «Федра» Delatte, Litt. 74f; однако, иконографический
мотив группы крылатых животных позаимствован с Востока, и

Вальтер Буркерт 95

Островам блаженных, за пределы Океана.
Путешествие в потусторонний
мир не вписывается ни в какие географические рамки. В любом случае,
представление о божественном происхождении и возвращении на небеса,
по крайней мере в зародышевом состоянии, было широко распространено задолго до времени Пифагора. Другой основой для такого представления служит обожествление звезд – идея, значение которой неминуемо
возрастает благодаря контакту с Вавилоном.299 Далее, связь между человеком и звездой300 является популярным верованием, которое принимает
специфическую форму в Египте,301 а также распространена вера в призраки, то есть в духов умерших, и их склонность бродить в атмосфере,

первоначально не имел никакого погребального смысла; см. иллюстрации,
опубликованные J. Boardman, Antike Kunst 10 (1967) pl. 2; но это приобретает
такой смысл к VI в. до н. э.; о бронзовой колеснице из Монтелеоне в НьюЙорке, см. R. Hampe and E. Simon, Griechische Sagen in der frühen etruskischen
Kunst (Mainz, 1964) 53–67; в целом, Meuli, Bachofen VII 498f; F. Matz, Gnomon
33 (1961) 63–65. Гиакинф и Полибия представлены на троне из Амикл
«идущими на небеса» (времена Креза: Paus. 3.19.4), хотя, в то же время,
Гиакинф получает свои смертные приношения через дверь в алтаре (Paus.
3.I9.3). Ср., также, Wuilleumier 357, 547ff.
299 Ср. Wilamоwitz, GldH I 253ff = I 248ff, 2nd ed.; Nilsson, Op. III 31–39.
Аристотель говорит («Метафизика» 1074b1), что ἀρχαῖοι καὶ παμπάλαιοι учили о
божественности звезд ἐν μύθου σχήματι, но поклонение звездам в основном
воспринималось как варварский знак (Ar. Pax 406, PI. Crat. 397d). О примере
восточного влияния на пифагорейцев см. выше, гл. II 4, сн. 47. Эсхил называет
звезды (Ag. 6) λαμπροὶ δυνάσται ἐμπρέποντες αἰθέρι.
300 Примеры от американских индейцев до австралийских аборигенов см. у
Фрезера (J. G. Frazer, The Golden Bough IV (London, 1911) 64ff); Capelle 19ff.
Распространены две версии. Либо душа умершего становится звездой, и падающая
звезда указывает, что эта душа спешит вернуться, либо живущий человек «имеет»
свою звезду, которая после его смерти угасает в виде падающей звезды. Как показал
Стенцел (Stenzel, KISchr 1ff; он сравнивает «Государство» 621b и Plut. De gеn. 22–
591c–d), первый вариант еще оказывал влияние на Платонов «Федр», а последний,
согласно Плинию (Plin. HN 2.28), – это взгляд простых людей (volgus); ср. Euseb.
Migne 86.1.453, Lucian's Lychnopolis, Ver. hist. 1.29, Boll, ZNTW 18 (1917) 40ff, Eur. fr.
971. Превращение умершего в звезду часто обыгрывается в погребальной поэзии (но
не в прозаических надписях; поэтическая форма допускает больше свободы): Peek,
nos. 1097, 1829, 1776, 648; Arch. eph. 1953–1954, 2, 290–296.
301 Умерший путешествует по небу в составе свиты солнечной ладьи (Plut. De
Is. et Os. 21; Kееs 42, 87ff). – Греческие катастеризмы (ассоциация душ со
96 Аст рономия и пифагореизм
особенно ночью, причем, каким-то мистическим образом, они особенно
тесно взаимодействуют с Луной.302 И, наконец, известна иранская концепция души, совершающей путешествие на небеса.303 Определение места
Пифагора и пифагорейцев в этом запутанном клубке – это вопрос, который может быть решен не посредством общих рассуждений, но только
путем анализа свидетельств.
В V веке до н. э. мы встречаем множество упоминаний об астральном
бессмертии. Аристофан ссылается на доктрину о том, что люди после
смерти становятся звездами;304 Алкмеон ставит вечное движение «божественных» звезд в один ряд с движением души, чтобы подтвердить ее
бессмертие,305 а Еврипид говорит, что Елена была перемещена в «чертоги Кронида» за пределы звездного неба.306 Эта идея часто выражает то,
что человек состоит из тела и души, и после смерти тело возвращается в

звездами) восходят к очень раннему периоду; это засвидетельствовано, по
крайней мере, для Медведицы и Ориона (Hes. frr. 148, 163), хотя имеются и
исключения.

Сказки - жемчуга мира
Книги Семи Морей

Шахерезада

Дата: Четверг, 2023-02-09, 4:47 PM | Сообщение # 23

Хранитель Ковчега

Группа: Проверенные

Сообщений: 3891

Статус: Offline

по документу - http://schole.ru/gallery/schole-suppl-1.pdf

302 Ср. Capelle 3ff; Cumont, Symb. chs. II—III. Не ясно, насколько в глубь веков
уходит отождествление Гекаты с лунной богиней (Norden, Vergil VI 23f, а Кереньи
(Kerényi 79f) находит это еще в гомеровском гимне (Hymn. Hom. Cer. 52)), или
отождествление щита Афины с головой Горгоны (Gorgoneion) с Луной (Meuli,
Bachofen VII 497f).
303 Выше, гл. IV 1, сн. 57.
304 Аристофан «Мир», 832–837: раб спрашивает Тригея после его
возвращения с небес, правда ли, что умершие, как говорят, становятся звездами.
Тригей отвечает, что это действительно так, и что Ион Хиосский, который
написал поэму об утренней звезде, после своей смерти был принят на небе как
ἀοῖος ἀστήρ. Это не основано на чем-то еще, кроме поэмы Иона; а в пользу
утверждения, что Ион был «пифагорейским поэтом» (Cumont, After-Life 95; Capelle 24f), один лишь факт упоминания им Пифагора во 2 и 119 фрагментах (в
собрании Блюменталя) предоставляет слишком шаткое основание (выше, гл. II
3, сн. 13, 51).
305 Выше, гл. III 3, сн. 97. Этимологии слов θεός : θεῖν и αἰθήρ : αἰεὶ θεῖν (Платон
«Кратил» 397c, 410b), вероятно, относятся к чему-то раннему – может к
Алкмеону, а может даже к ионийцам (ниже, сн. 60). Пифагорейцы,
интерпретируя пылинки в солнечном луче, считали движение существенной
характеристикой души (Аристотель «О душе» 404a16ff; ср. выше, гл. II 4, сн. 138).
Такая же идея была у Анаксагора и Демокрита (Аристотель «О душе» 403b20ff).
306 Eur. Or. 1683–1690.
Вальт ер Бурк ерт 97
землю, а душа в небесный эфир, откуда она родом. В эпиграмме, посвященной тем, кто пал при Потидее (432 г. до н. э.), этот взгляд приобретает квази-официальное признание.307 Он появляется не только у Еврипида, но и у Эпихарма, что, по всей видимости, прямо указывает на
пифагорейское происхождение. Но в традиции Еврипид во многих отношениях связывается с Анаксагором.308 Последний говорил об «эфирном зное» (aetherius calor) в эмбрионе – поскольку жизнь происходит от
«теплого» эфира. 309 Для Диогена Аполлонийского душа была частью
«божественного» воздуха и, таким образом, μόριον θεοῦ. 310 Анаксагор
также считал душу бессмертной,311 и это причина, по которой они оба
ставятся в один ряд с Пифагором. Медицинские авторы воспроизводят
такие же верования.312 Но даже у Левкиппа и Демокрита душа является

307 IG I
2
945 = Peek no. 20 line 5: αἰθὲρ μὲμ φσυχὰς ὑπεδέχσατο, σό[ματα δὲ χθόν];
Epicharm. DK 23B9: συνεκρίθη καὶ διεκρίθη κἀπῆλθεν ὅθεν ἦλθεν πάλιν. γᾶ μὲν εἰς γᾶν,
πνεῦμα δ᾽ ἄνω, ср. фр. 22; Eur. Supp. 531ff: ἐάσατ᾽... ὅθεν ἕκαστον ἐς τὸ φῶς ἀφίκετο,
ἐνταῦθ᾽ ἀπελθεῖν. πνεῦμα μὲν πρὸς αἰθέρα, τὸ σῶμα δ᾽ ἐς γῆν, Eur. Erechtheus fr. 65.71f
Austin: ψυχαὶ μὲν οὖν τῶνδ᾽ οὐ βεβᾶσ᾽ Ἅιδην πάρα, εἰς δ᾽ αἰθέρ᾽ αὐτῶν πνεῦμ᾽ ἐγὼ
κατῴκισα. Ср. Supp. 1140, Hel. 1013ff (душа и эфир бессмертны), фр. 839, 877, 971
(также Rohde, Psyche II 255f = 435f, анг. изд.). Такая же концепция в других
надгробных надписях: IG II/III2
11466 = Peek no. 1755 (начало IV в. до н. э.), 12599
(Peek, no. 1759, 3 в. до н. э.); Peek nos. 1760–1761.—Hippoc. Hebd. 52 = Aph. 8.12
(VIII 672 L.).
308 Eur. fr. 839 = Anaxagoras A112, lines 8ff:
χωρεῖ δ' ὀπίσω
τὰ μὲν ἐκ γαίας φύντ' εἰς γαῖαν,
τὰ δ' ἀπ' αἰθερίου βλαστόντα γονῆς
εἰς οὐράνιον πάλιν ἦλθε πόλον·
θνῄσκει δ' οὐδὲν τῶν γιγνομένων,
διακρινόμενον δ' ἄλλο πρὸς ἄλλου
μορφὴν ἑτέραν ἀπέδειξεν.
309 Анаксагор A109. Фридрих (W. H. Friedrich, Philologus 97 [1948] 281f)
автором этой идеи считает Анаксагора.
310 Диоген Аполлонийский A 20, 19 §42.
311 Aёt. 4.7.1.
312 Напр., Hippoc. Carn. 2 (DK 64C3): ἀθάνατον θερμόν, которое «мыслит,
видит, слышит и знает все»; большинство из этого «продвинулось к крайней
окружности, и это то, что древние, как я считаю, называли αἰθήρ». – Концепт
«мировой души» (который ван дер Варден, например в Astr. 25, считал
специфически пифагорейским, по контрасту с ионийскими физиками) сводится
98 Аст рономия и пифагореизм
«огненной», как Солнце и Луна,313 так что Лукреций, придерживаясь материалистической традиции, заимствовал выражения у Еврипида. 314
Душа была «огнем» у Парменида и Гиппаса,315 говорят, что и Гераклит
называл ее scintilla stellaris essentiae.316 И еще до Анаксимена ψυχή была
связана с «божественным» воздухом, который окружает и поддерживает космос.317
То, что душа человека тесно связана с небесами и звездами, и даже
то, что она приходит с небес и туда же возвращается, является верованием, общим для ионийской «физиологии» (φυσιολογία), по крайней
мере, со времен Гераклита и Анаксагора.318 В «физиологическом» облачении и с помощью «материалистической» фразеологии то, что началось в виде «мифа» (μῦθος), продолжает позже оказывать свое влияние,
иногда с большим ударением на спасение души, а иногда – на общие

к таким доктринам. Согласно Платону («Кратил» 412d–e) «многие» верят в
διεξιόν, который пронизывает весь мир, и иногда называется Солнцем, иногда
θερμόν, а иногда νοῦς. Из окружения Диогена происходят выражения, вроде Ar.
Nub. 229ff; и у Платона в «Кратиле 396с (муза Οὐρανία это ὁρῶσα τὰ ἄνω, ὅθεν δὴ
καί φασιν...τὸν καθαρὸν νοῦν παραγίνεσθαι οἱ μετεωρολόγοι) высказывание так же
не является просто «пифагорейским» (pace Boyancé, REG 1941, 156f; Joly 36f). –
«Божественное» θερμόν как ψυχῆς δύναμις, ἀνάλογον οὖσα τῷ τῶν ἄστρων
στοιχείῳ признается Аристотелем (Gen. an. 736b29ff, о чем см. F. Solmsen, JHS 77
[1957] 119–123; H. A. T. Reiche, Empedocles' Mixture, Eudoxan Astronomy, and
Aristotle's Connate Pneuma [Amsterdam, 1960] 97ff; Arist. Περὶ φιλοσοφίας fr. 27 W.
= Cic. Acad. 1.26).
313 Левкипп A 28, Демокрит A 101–102; ср. D.L. 9.44.
314 Лукреций 2.991ff, после Еврипида, фр. 839.
315 DK 18.9, 28 A 45; ср. 46а–b.
316 Гераклит A 15: νοῦς относится к περιέχον; A 16 §129ff, ср. А 17:
возвращение души πρὸς τὸ ὁμογενές. По всей видимости, здесь затрагивается
стоическая интерпретация и систематизация; Гераклит говорит о «смерти»
души (фр. 36), или, по меньшей мере, некоторых душ (ср. Kirk in KR 205ff).
317 Анаксимен, фр. 2, и J. Longrigg, Phronеsis 9 (1964) 1–4. θεῖον περιέχον
(ἄπειρον) уже представлен а Анаксимандра.
318 «Здесь нет ничего пифагорейского», говорит Нестл (Nestle, ZN I 610 n. 1)
о фрагментах Эпихарма. С другой стороны, Пфайфер (Pfeiffer, Sterngl. 114)
утверждает, что Гераклит приписывал «важные черты своего мировоззрения»
Пифагору. Это выглядит неприкрытой критикой Платона, которая не
позволила исследователям развить тот же тезис в отношении Анаксагора.
Вальт ер Бурк ерт 99
представления о микрокосме и макрокосме: человек сделан из частей
космоса и после смерти желает в него же вернуться.319
Если все эти представления в целом можно было бы возвести к Пифагору, то пришлось бы приписать его учению максимум влияния и минимум определенного содержания, поскольку свидетельства в высшей
степени разрознены. Известная Эпихарму 320 божественность звезд и
аналогическое заключение Алкмеона настолько же далеки от идеи, согласно которой душа сделана из небесного огня, насколько далеки от нее
незамысловатые представления о том, что души становятся звездами. И
все эти противоречивые идеи в тот или иной период приписывались
Пифагору.321 Но в описанном Пиндаром метемпсихозе не больше следов небесных мотивов, чем в теории Эмпедокла о падшем демоне, со-

319 Уже в Ригведе; см. H. v. Glasenapp, Die Religionen Indiens (Stuttgart, 1943)
84; Olerud 153. Платон в «Тимее» 63c намерено ограничивает эту «теорию
исчезновения» вещества.
320 Менандр, фр. 614 Körte: ὁ μὲν Ἐπίχαρμος τοὺς θεοὺς εἶναι λέγει ἀνέμους,
ὕδωρ, γῆν, ἥλιον, πῦρ, ἀστέρας. Несомненно, это меньше похоже на древнее
благочестие, чем зарождающийся скептицизм; впоследствии, никто больше не
верит в мифических богов, и ограничивается наблюдаемым.
321 Hypomn. 27: Солнце, Луна и звезды считаются богами из-за действующего в
них θερμόν. Душа это ἀπόσπασμα αἰθέρος, она бессмертна (28) и невидима (30). После
смерти она парит в воздухе до тех пор, пока Гермес не сопроводит непорочные души
ἐπὶ τὸν Ὕψιστον (об этом выражении см. Cumont, Or. rel. 58, 273 n. 93; RE s.v.
Hypsistos; Cook, Zeus II 876ff; Целлер (Zeller III 2.106, n. 2) едва ли прав, видя в этом
иудейское влияние). – Varro in Comm. Bern. Luc. 9.9 p. 291 Usener: «Pythagoras dixit
animas in Stellas converti virorum fortium" (Varro Antiq. rer. div. fr. 25b Agahd; но, см.
Reinhardt, RE XXII 589). – Плутарх изображает картину астрального бессмертия в
диалоге о демоне Сократа, действующие лица которого принадлежат к
пифагорейской группе в Фивах (выше, сн. 39). – О Луне как жилище душ см. ниже,
сн. 75; о Млечном пути и вратах в рай, ниже, сн. 90, 94.
100 Аст рономия и пифагореизм
сланном на Землю в «пещеру» (он помещает Аид в пространство воздуха). 322 В памятниках южноитальянской эсхатологии нет никаких
надежных ранних свидетельств о вере в небесное бессмертие.323

Остается рассмотреть акусму, которая задает вопрос: «Что есть Острова блаженных?», и отвечает: «Солнце и Луна».324 Акусма помещает потусторонний мир в упорядоченном космосе, и является проявлением
той же страсти к стабильности, которая мастерит теологию души из
мифа о душе и налагает ритуальные табу на «образ жизни» (βίος). Высота и глубина, падение и восхождение не становятся доминирующими

322 Ср. выше, сн. 38, и гл. II 3, сн. 80. ἄντρον, Эмпедокл, фр. 120; во фр. 6
Ἀιδωνεύς это воздух, а Гера – Земля; ср. папирус из Дервени, col. 18.7. Об
интерпретации «Аида», Cumont, Symb. 35ff, Lux 189ff, Nilsson II 228ff. Возможное
решение: Аид может быть ночной половиной небесной сферы (выше, гл. IV 3,
сн. 64); это может быть Луной и подлунной областью (ниже, сн. 89, 93); или это
может быть жизнью на Земле (Lucr. 3.978–1023; ср. полную трактовку у Carcopino, Bas. 264ff.) – Различение подлунного и надлунного миров
приписывается Эмпедоклу (A 62), а также Алкмеону и Гераклиту (ср. выше, гл.
III 2, сн. 32), но мы не можем предполагать, что Эмпедокл придерживался
поздней доктрины о вечном, совершенном порядке небесной области; его
космос уничтожим и предопределен стать частью совершенной единой
«Сферы».
323 Диск из Бриндизи, изображающий путешествие умершего героя по
зодиаку, не поддается датировке (Wuilleumiеr 544ff, pl. 45, со ссылками). Он
датирует его периодом до римского завоевания, то есть, как минимум, III веком
до н. э. Похожие мотивы можно найти и на других дисках из Тарента, но на них
нет зодиака. – На вазах из Каносса (III в. до н. э.), ставших знаменитыми
благодаря Бахофену (Bachofen), однозначно не представлено астрального
символизма (Meuli, Bachofen VII 493ff). – Следы астрального бессмертия на
золотых пластинах также неоднозначны (αὐτὰρ ἐμοὶ γένος οὐράνιον, DK 1B17.7,
из Петелии; ἱμερτοῦ δ᾽ ἐπέβαν στεφάνοθ, DK 1B18.7, из Турий, см. Carcopino, Bas.
314f, и Diels, DK I 16 n.; A. Dieterich, Kl. Schr. 95 сравнивал Orph. Arg. 761, но в
следующем стихе Персефона называется χθονία βασίλεια). – Сбивающее с толку
заключение, ἔριφος εἰς γάλα ἔπετον, Дитрих интерпретировал как указание на
Млечный путь (A. Dieterich, De hymnis Orphicis (Marburg, 1891) 35ff = Kl. Schr.
95ff; более решителен Carcopino, Bas. 311ff, Wuilleumier 547f. Против S. Reinach,
Cultes, mythes et religions II2
(Paris, 1909) 125ff; K. Wyss, Die Milch im Kultus dcr
Griechen und Römer (Giessen, 1914) 53ff. Слово ἔριφος указывает на Диониса (ср.
выше, сн. 45).
324 Iam. VP 82 (выше, гл. II 4).
Вальт ер Бурк ерт 101
идеями в теологии души до тех пор, пока пространство звезд не становится частью единой картины. К этому же относятся и представление о
том, что Большая и Малая Медведица – это руки Реи, Плеяды – лира
Муз, планеты – псы Персефоны, землетрясения – тайное собрание мертвецов, и целью грома является испугать тех, кто наказан в Тартаре. В
этом контексте считается несомненным, что Аид находится под землей,
и все упоминания о пифагорейском katabasis производят то же впечатление.325 Вывод о том, что, согласно новым астрономическим данным,
Аида не существует, пифагорейцев не привлекал. Острова Блаженных
не являются частью Аида; они расположены далеко от страны мертвых.
Душа отправляется на Острова, в место своего последнего отдыха, где
она, несомненно, слышит «гармонию Сирен». 326 Отделение Островов
блаженных от мира умерших имеет древнее происхождение, и вероятно, было одной из ранних форм школьной доктрины. Поэтому общая
картина, вкупе с акусмами, становится осмысленной. Такие представления полностью чужды астрономии, насколько об этом можно судить по
объединению «Солнца и Луны», как если бы они были островами одного моря. Здесь нет никакого намека на привычное для поздней античности представление о многоуровневом космосе.327 И снова мы видим,
что акусмы представляют собой независимую от поздней традиции
точку зрения, равно как и от Эмпедокла и Платона,328 и показывают пифагореизм, еще ничего не знающий о научном восприятии мира.

325 Выше, гл. II 3. Carcopino, Bas. 272 n. 4, видит здесь соскальзывание к
примитиву со стороны акусматиков.
326 Выше, сн. 3, 37. Определенное значение можно придать тому факту, что
Гомер («Одиссея» 12.52, 167) безошибочно говорит о двух Сиренах.
327 Луну довольно часто называют Островами блаженных (ссылки у Capelle
10ff; Cumont, Symb. 177ff; Nock, AJA 1946, 142f), например Кастор Родосский (1
в. н. э., FGrHist 250F16 Plut. Quaest. Rom. 76.282a, Plut. De fac. 29, Рог. ар. Stob.
1.49.61, Serv. Aen. 6.640, 887). Однако Луна часто является промежуточной
остановкой, а Солнце следующая высшая стадия (Plut. De fac. 29.944c, Amat.
20.766b, Рог. ар. Stob. 1.49.55). Только в Comm. Bern. Luc. 9.9 (Посидоний,
согласно Reinhardt, RE XXII 589f, 780) Солнце и Луна находятся на одном
уровне: душа возвращается «in suam sedem, hoc est in solis globum ac lunae».
Рейнхард (Reinhardt, Kosmos 312 n. 2) сомневается в древности пифагорейской
акусмы.
328 О связи акусм с Алкмеоном, Эмпедоклом и Филолаем трудно сказать что либо определенное;

конец цитаты

Сказки - жемчуга мира
Книги Семи Морей

Сообщение отредактировал Шахерезада - Четверг, 2023-02-09, 4:51 PM

MгновениЯ

Дата: Пятница, 2023-03-10, 8:24 PM | Сообщение # 24

Ковчег

Группа: Администраторы

Сообщений: 18316

Статус: Offline

цитата

Геометрия становится музыкой

Ранее мы рассматривали теорию разделения единства на множество с точки зрения двух аспектов:

идея наличия некоторой корневой функции, основанной на квадратных корнях из 2 и 5;

идея взаимных идеальных отношений из трех или четырех шагов, рассчитанных из указанных корней.

В этой главе мы рассмотрим идеи корней, прогрессий и отношений совместно с тем, чтобы еще раз досконально выявить все взаимосвязи между ними. При этом свое исследование мы будем вести путем выявления связей между геометрическими пропорциями и музыкальной гармонией. Надеемся, что это исследование прольет свет на высказывание Гете, что «геометрия – это замороженная музыка».

Начать данное исследование стоит с теории отношений, являющейся краеугольным камнем античной философии и заключенной в простом наблюдении за взаимным поведением членов функций. Возвращаясь к нашей дискуссии по поводу пропорций из трех или четырех членов (стр. 44) и используя ее в качестве отправной точки, мы обратимся к предупреждению Платона, что сравнение функций из четырех членов, не дает непрерывного ответа, то есть имеет дискретный характер. Это предупреждение до сих пор остается полем, открытым для споров. Такое утверждение еще называют «дискретным знанием». В противовес этому Платон вводит термин «непрерывное знание», которое не является простой суммой накопленных фактических и теоретических знаний об окружающем мире, но представляет собой мысленное постижение метафизических законов, стоящих за физическим миром. Метафизические законы, по которым конструируется форма и поведение всех объектов, являются действительной целью исследователя, желающего приобрести не фрагментарное, а полное или «непрерывное» знание об окружающем мире. Такие законы, согласно Платону, могут быть открыты благодаря изучению отношений или связей между двумя крайними феноменами, определяющими их взаимное поведение. Ранее мы уже изучали такую систему отношений между тремя членами – a : b :: b : c – выраженную через геометрическую прогрессию, именуемую греками «логосом». Но этот простой пример расскажет нам не только о взаимной системе отношений трех членов прогрессии. Наука Отношений изучает систему пропорциональных отношений не столько между указанными тремя членами, сколько поведение самой этой системы, как отдельного объекта для исследования, раскрывающего нам суть различий между этими тремя членами.

Пропорция отношений может быть выражена как А-группа трех неравных чисел, и двух отношений или связей каждого из этих чисел к остальным, а также каждого из чисел по отношению к самому себе.

Этот странный математический «коан» (коан – короткое парадоксальное высказывание в дзен-буддизме, используемое в качестве умственного упражнения, прим. перев.) содержит в себе три вида прогрессии, через которые могут быть выражены связи – Арифметическую, Геометрическую и Гармоническую.

Давайте попробуем выразить эту трехступенчатую систему отношений (иначе -медиан) по шагам. Итак, медианная пропорция формируется в группе из трех чисел (a, b, c). При этом a больше, чем b, а b больше, чем c (a>b>c). Тогда система отношений или разниц выражается следующим образом:
a-b,
b-c.

Тогда выражение взаимных отношений будет выглядеть как:
a-b : b-c,

а отношение каждого числа в последовательности к самому себе будет выражаться так (вариант 1):
a-b : b-c :: a : a, b : b, c : c

а отношение каждого из этих числе к двум другим будет выражаться так:

(вариант 2) a-b : b-c :: a : b или
(вариант 3) a-b : b-c :: a : c.

В первом варианте решение выражения по отношению к b будет выражаться следующим образом:
b = (a + c) / 2,
что является формулой арифметической прогрессии. Числа арифметической прогрессии 3, 5, 7 будут получены при основании прогрессии b = 5.

Во втором варианте решение выражения по отношению к b будет выражаться следующим образом:

или

что является формулой геометрической прогрессии. Числа прогрессии 4, 8, 16 будут получены при основании прогрессии b = 8.

В третьем варианте решение выражения по отношению к b будет выражаться следующим образом:
b = 2ac/(a+c),
что является формулой гармонической прогрессии. Числа прогрессии 2, 3, 6 будут получены при основании прогрессии b = 3.

Эти три варианта выражения отношений дают нам полную математическую формулу выражения всех типов связей. Арифметическая пропорция выражает закон сложения и обратного ему вычитания, и описывает систему связей, дающую серию натуральных чисел 1, 2, 3, 4, 5, 6 и так далее. Геометрическая пропорция выражает закон умножения и обратного ему деления, и дает на выходе различные варианты геометрических серий чисел. Здесь мы должны добавить, что добавление и умножение – есть два способа математического выражения стремления к росту в природе. Гармоническая пропорция является следствием комбинации первых двух. Она формируется путем умножения двух экстремумов (a, c) и последующего деления их среднего значения или арифметического основания (a + c) / 2. Для примера возьмем два экстремума 6 и 12, их умножение даст нам цифру 72, среднеарифметическое между ними – 9, а 72/9 = 8. Таким образом мы получаем гармоническую пропорцию 6, 8, 12.

Арифметическая пропорция:

Геометрическая пропорция:

Гармоническая пропорция:

Каждая из указанных видов пропорций имеет набор уникальных характеристик. Например, арифметическая прогрессия демонстрирует равенство разностей, но неравенство отношений. Например, для арифметической последовательности: 3, 5, 7 будет справедливо следующее:

С другой стороны, геометрическая прогрессия демонстрирует равенство отношений, но неравенство разностей. Например, для геометрической последовательности: 2, 4, 8 будет справедливо следующее:

Наиболее важной и отчасти мистической характеристикой гармонической пропорции является тот факт, что инверсия любой гармонической прогрессии будет равна арифметической прогрессии. Например, последовательность 2, 3, 4, 5 – нарастающая арифметическая прогрессия, а ее инверсное значение – 1/2, 1/3, 1/4, 1/5 – убывающая гармоническая прогрессия. В музыке такое инверсное отношение между арифметической и гармонической прогрессиями означает, что два экстремума двойных отношений дают нам двойную октаву, что в итоге дает нам прогрессию, именуемую «музыкальной пропорцией»: 1, 4/3, 3/2, 2. Другими словами арифметическая и гармоническая разность между двойными геометрическими отношениями представляет собой числовую последовательность, соответствующую тональным интервалам звукового ряда «чистая кварта» (perfect forth) и «чистая квинта» (perfect fifth) – базовые консонансы практически во всех музыкальных звуковых рядах (консонанс – благозвучно звучащее сочетание звуков в музыке, прим. перев.).

Базовая структура пропорций, которую мы используем в нашей математике, также представляет собой базовую структуру в сфере музыки. Давайте исследуем роль этих пропорций, как основных архетипов, создающих все виды форм во Вселенной музыки.

Прогрессия 1, 4/3, 3/2, 2 – демонстрирует нам частоты основного тона, кварты, квинты и октавы. Затем мы обратим внимание на арифметические и гармонические пропорции между длинами струн, равными 1 и 1/2. Деление струны пополам дает нам октаву, или звук в два раза большей частоты, нежели основной тон. Основание гармонической прогрессии между 1 и 1/2=2/3, дает музыкальную квинту, а основание арифметической прогрессии между 1 и 1/2=3/4 – музыкальную кварту. Если мы сравним эти две прогрессии, то мы увидим инверсию их коэффициентов и пересечение функциональных позиций между арифметическим и гармоническим основаниями.

Рисунок 1.
Деление гитарных струн.
Перевод надписей: Fundamental – основной тон, Fourth – кварта, Fifth – квинта, Octave – октава, Harmonic – гармоническая прогрессия, Arithmetic – арифметическая прогрессия.

Примечание.

Музыкальная октава представляет собой деление основного тона (гитарной струны, например, прим. перев.) пополам, и соответственно ее частота в два раза выше этого тона. Например, если на гитаре мы дернем первую струну, то мы услышим основной тон, в музыкальной нотации соответствующий ноте МИ (E). Для простоты расчетов присвоим этой ноте цифру 6, обозначающую количество вибраций в секунду (в действительности 82,5) (речь идет о ноте МИ большой октавы, имеющей частоту 82,41 Гц, прим. перев.). Теперь если мы задержим наш палец на ладу, помеченном как E’ (МИ, прим. перев.), что находится ровно посередине нашей струны, то частота вибрации этой струны возрастет ровно в два раза. Полученное значение вибраций арифметически относительно нашего основания, равного 6-ти, станет равным 12-ти, то есть 2:1. Октавный звук имеет одну странную характеристику, он имеет в два раза более высокую частоту, но слышится при этом как основной тон. Опыт прослушивания октавы содержит в себе одновременное ощущение схожести и разницы звуков, по сравнению с основным тоном. Эта особенность восприятия культивируется в сакральной геометрии: нечто разделенное, но гармонично соединяемое вместе.

Аналогично, если мы поместим наш палец на гитарный лад СИ (вторая струна на гитаре, прим. перев.), то струна СИ будет звучать по отношению к струне МИ как 3:2, или по нашей калькуляции – 9:6. Полученный тон СИ является приятным на слух консонантом и именуется музыкальной квинтой (в английской нотации – музыкальная «пятая» – musical fifth, прим. перев.), потому что это пятый тон в натуральном звуковом ряде (если принять за единицу число колебаний первого звука (основного тона) струны, то числа колебаний частичных тонов выразятся рядом простых чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 и т. д. Такой ряд звуков называется натуральным звукорядом. Прим. перев.), диатонический мажорный лад, с МИ как ДО, а СИ как СОЛЬ. На гитаре мы получаем звукоряд, состоящий из восьми натуральных тональных деления от МИ до МИ, именуемых «октавами». Если мы положим палец на лад ЛЯ струны ЛЯ, это даст другой вид консонанса, именуемый квартой, и его отношение частот будет соответствовать 4:3, или 8:6 в нашей нотации.

Загадка музыкальной гармонии, заключенная в одновременной инверсии, также содержит в себе добавление и умножение. Октава основного тона может быть получена путем сложения интервалов: длина строки, составляющая сумму квинты и кварты, составляет октаву, а умножение частоты вибраций кварты и квинты также сформирует нам октаву (4/3х3/2=2). Комбинированный эффект добавления и умножения в математике даст нам логарифм, который, как мы видели ранее, является основанием Золотого Сечения в архитектуре.

Нижеследующая таблица демонстрирует скрытую тайну законов звука, заключенную в том, что возрастающие числа, демонстрирующие отношения звуковых частот, соответствуют обратному порядку длин струн. Закон музыкальной гармонии, рассматриваемый с точки зрения идеи частотных пропорций, неожиданно становится законом естественного порядка во Вселенной, некоем Дао всех вещей, согласно которому обратные друг другу одновременные движения влияют друг на друга с тем, чтобы создавать звук и все видимые формы.

Рисунок2.
Таблица отношений частот звуковых волн и длин струн.

Перевод надписей: Vibration – колебания. Note – нота. H M (Fourth) – кварта. A M (Firth) – квинта. Octave – октава. String length – длина струны.

Теперь мы готовы продемонстрировать этот числовой и гармонический принцип в геометрии. Геометрическое основание может быть выражено формулой:

Тогда гармоническое основание может быть выражено формулой:
b(a+c)=2ac,
и таким образом является результатом сложения двух экстремумов, что может быть выражено как:

.

Геометрическая пропорция также называется идеальной пропорцией потому, что она прямо-пропорциональна и ограничена одним средним значением. И арифметическая и гармоническая медианы представлены в этой геометрической пропорции посредством взаимного обмена противоположностей, игрой между чередованием и инверсией.

Практические примеры
Давайте попробуем найти доказательства нашей теории о прогрессиях и гармонии в музыке, о которых говорили выше. Для начала возьмем две геометрических прогрессии начинающиеся с цифр 2 и 3 с шагом 2. Первый член прогрессии – 2 будем именовать мужским, а 3 – соответственно женским. Соотношение 1:2 символизирует октаву, пространственная среда, в которой первое консонантное деление на три (квинта 2/3) символизирует начало или определение шаблона будущей формы, то есть некоего правила или формулы, задающей фиксированные пропорции в изначально безбрежном и необусловленном звуке – октаве.

3 6 12 24 48
2 4 8 16 32

В работе Платона «Тимей» продемонстрирован тот факт, что посредством умножения цифр 2 и 3 можно выразить все цифры в Пифагорейской музыкальной системе, состоящей из квинт 3:2. Как платонисты мы помним, что цифра Два символизирует силу умножения, октаву, женское начало, изменчивость, в то время как цифра Три символизирует мужское начало, точность, твердость, устойчивость к изменениям, неизменный источник шаблонов построения форм, таблица умножения на которую даст нам все доступные виды музыки. Так была описана в его работах «музыка сфер», как универсальная гармония, возникающая между этими двумя символами женского и мужского начала.

Рисунок 3.

Эта диаграмма Джорджи (Франческо Георгий Венето (Джорджи) (1460-1540), итальянский францисканский монах и автор работы De Harmonia Mundi Totius, прим. перев.) показывает две геометрических прогрессии, начинающихся с цифр 2 и 3 и данных Платоном в «Тимей», демонстрирует их связь с музыкальными пропорциями 6, 8, 9, 12. Он использовал музыкальные пропорции в качестве основания для расчета оптимального количества октав, кварт и квинт, формирующих гармоническую систему, которую можно использовать в архитектуре, изобразительном искусстве и других видах творчества.

Желаю Счастья! Сфера сказочных ссылок

MгновениЯ

Дата: Пятница, 2023-03-10, 8:24 PM | Сообщение # 25

Ковчег

Группа: Администраторы

Сообщений: 18316

Статус: Offline

Теперь давайте попробуем интерпретировать эти две геометрические последовательности, и выясним, что геометрическая
прогрессия на самом деле является комбинацией арифметической и гармонической прогрессий.

Рисунок 4.
Комбинация прогрессий.
Перевод надписей: Arithmetic – арифметическая прогрессия, Harmonic – гармоническая прогрессия.

На рисунке мы видим, что каждое перекрытие наборов из трех чисел дает нам либо арифметическую, либо гармоническую
прогрессию: 2, 3, 4 – арифметическая, 3, 4, 6 – гармоническая; 4, 6, 8 – арифметическая, 6, 8, 12 – гармоническая и так
далее. Таким образом перемешивание мужского числа, рассчитанного в геометрической прогрессии, и женского числа,
рассчитанного также, дает нам в итоге два перемежающиеся числовых ряда, составляющих интересную пропорцию.

Давайте теперь попробуем использовать тот же подход, использованный в одномерной линейной структуре, в структуре
двумерной, в виде Лямбда Таблицы (такую таблицу также иногда называют «лямбдома», и она представляет собой
тетрактис Пифагора, дополненный лямбдой из диалога Платона «Тимей», посвященный происхождению и устройству
Вселенной, прим. перев.):

Это треугольный массив чисел, которые пересекаются в геометрической прогрессии от 2 (по горизонтали) и от 3-х (по
диагонали). Все последующие вертикальные числа соотносятся друг к другу как 2:3, что аналогично умножению одного
числа на 3/2 для того, чтобы получить следующее число. Это последовательное умножение на 3/2 (музыкальную квинту) и
есть тот метод, что был использован Пифагором для формирования музыкального звукового ряда. Характеристики числовых
рядов, указанные на страницах 82 и 83 (в нашем случае в данной статье, прим. перев.), теперь становятся очевидными.

Генеративный характер Лямбда Таблицы изображен на бедрах женщины в работе 1503 г. на странице 7. Исследуя данную
таблицу мы обнаруживаем, что каждый квадрат из четырех чисел, например 2, 4, 6, 3, содержит в себе две арифметических
прогрессии (2, 3, 4 и 2, 4, 6), дающие нам три грани квадрата (кроме нижней грани) и одну диагональ. Кроме того,
аналогичная фигура получается из гармонической прогрессии 2, 3, 6 и 3, 4, 6, что дает нам три стороны квадрата, две из
которых совпадают с квадратом предыдущим, а третья проходит внизу, а также диагональ.

Рисунок 5.
Квадраты арифметической и гармонической прогрессии.

Эту таблицу дал нам Никомах Герасский (древнегреческий философ, математик, теоретик музыки, 60-120 г. н.э., прим.
перев.), в ней наложены указанные две пропорции, дающие нам квадрат, как конечный символ, выражающий базовые
основы существования реальности. Это выраженное графически соответствие между числами и музыкальными
пропорциями, указанное в «Тимей», и способ, которым Мировая Душа проявляется в физическом мире.

Другое геометрическое упражнение показывает связь между исходными функциями и медитативными практиками,
создающими мир гармонии в музыке.

Рисунок 6.

Используя квадрат со сторонами и площадью, равными единице, мы можем дать геометрическое или
тригонометрическое доказательство того факта, что если от пересечения диагонали квадрата с длиной линии
равной √2 с линией, и линии с длиной √5/2 провести линию под прямым углом к верхней грани квадрата, то
мы получим деление этой грани на части, равные 1/3 и 2/3. А в итоге мы получим трехступенчатую
арифметическую прогрессию: 1/3, 2/3, 1.

Рисунок 7.

Снова вернемся к этому квадрату. Теперь нарисуем дугу по окружности из левого нижнего угла в правый
верхний угол. Снова найдем точку ее пересечения с диагональю √2. Из полученной точки нарисуем новую дугу
относительно левой верхней вершины квадрата с вычисленным через пересечение радиусом. В итоге мы снова
получим деление верхней грани квадрата, но теперь в трехступенчатой гармонической прогрессии: (√2-1),(2-
√2),1.

Рисунок 8.

Последний способ деления квадрата со стороной, равной 1, приведет нас прямая с длиной √5⁄2. Эту прямую мы
проведем из левого верхнего угла в середину правой грани. Далее из правого верхнего угла мы нарисуем дугу
из окружности, радиус которой также равен половине длины правой грани или 1/2. Из полученной точки
пересечения мы нарисуем новую дугу из окружности в центре верхнего левого угла. Пересечение этой
окружности с верхней гранью даст нам ее деление в соответствии с геометрической пропорцией: 1⁄(ϕ^2,1⁄(ϕ,1))
(где ϕ=(√5-1)/2=1,618 – постоянная «золотого сечения», прим. перев.).

В квадрате ABCD со сторонами, равными 1, диагонали проводятся через углы AC и BD. Если нарисовать окружность с
радиусом BD (как мы видели выше радиус в этом случае будет равен √2) и центром в точке B вниз от точки D, то мы
получим новую точку – G, отстоящую от B на √2. Дорисуем новый прямоугольник со стороной √2, получив точки G и H.
Далее нарисуем в точке С новую окружность с радиусом, равным длине грани СG, то есть разнице радиуса окружности √2 и
единичной стороны квадрата: √2-1. Пересечение этой окружности с диагональю единичного квадрата AC даст нам точку F.
Аналогичная окружность из точки D, пересекаясь с диагональю BD даст нам точку E. Далее из вершин единичного квадрата
A и B нарисуем новые окружности с радиусами AF=BE. Соединив полученные дуги и соответствующие им грани единичного
квадрата и нового прямоугольника мы получим изображение кубка (идеальный «Грааль»).

Рисунок 9.

Пример изображения красивого кубка или судна, нарисованного в стиле кубка, полученного путем
гармонического деления целой фигуры. Мы можем сказать, что видим здесь идеальное изображение Святого
Грааля.

Это кубок представляет собой пример analogos геометрической пропорции, выраженной путем деления изначально единой
фигуры на ряд средних и экстремальных значений.

Все три медианы были рассчитаны исходя из того, что единица принималась как наибольшее число из соответствующего
ряда. Эти ряды чисел провозглашены основой трансцедентальных (сверх-рациональных) пропорций, ввиду предположения,
что в неизмеримом состоянии они уже заложены в первоначальное единство, из которого исходят. (Нужно помнить, что
античная музыка построена только на целых числах, но основные принципы музыкальной структуры базируются на
показанных здесь правилах деления). Эти три медианы составляют собой триединство триединств, другими словами, это три
ступени деления каждой из трех видов прогрессий. Посредством священных корней из чисел 2 и 5 они выражают
гармоническое деление Времени (музыка) и Пространства (геометрия), и часто используются в традиционных культурах,
находя свое выражение в архитектуре, изобразительном искусстве, науке, мифологии и философии.

Комментарии к практическим примерам
Найденные Платоном гармонические соотношения, указывают на фундаментальную связь между музыкой и геометрией. В
своем «Седьмом письме» Платон указывал, что эта связь и есть фундаментальное знание, над достижением которого
действительно стоит работать. И возможно именно по данным законам египтяне построили две свои пирамиды в Гизе, в
основе которых геометрическая прогрессия 1,√ϕ,4, используемая при расчете размеров граней треугольников на сторонах
одной пирамиды, а арифметическая прогрессия 3, 4, 5 другой. В наши дни Симона Вэйль (Simone Weil) (Симо́на Адольфи́на
Вейль (Вайль) — французская религиозная мыслительница и философ, 1909-1943 г., прим. перев.) указывает, что весьма
важно исследовать эти законы, лежащие по ее мнению в основе христианского мистицизма.

Посредством работ Ханса Дженни (Hans Jenny) (швейцарский исследователь, придумавший термин «киматика», 1904-1972
г., прим. перев.) мы можем воотчую лицезреть прямую связь между формой и звуком в физическом мире. Эксперименты
Дженни показали нам, что частоты звуковых волн имеют способность влиять на хаотичное движение частиц или строить
различные формы из плотных изначально бесформенных эмульсий. Создавать периодически повторяющиеся
последовательности. Другими словами звук – это инструмент посредством которых временные шаблоны могут сформировать
пространственные и геометрические формы.

Рисунок 10.

Планетарная система базируется на музыкальной пропорции 6, 8, 9, 12, построенной на арифметической и
гармонической прогрессиях, между геометрическими соотношениями 6 и 12, в которой все тона построены на
Пифагорическом диатоническом (мажорном) звукоряде (его также называют «Пифагоров строй», прим.
перев.) (к сожалению найти данное изображение в хорошем качестве с читаемыми надписями автору перевода
не удалось, если у кого-то получится, то пришлите пожалуйста для публикации.

Связь между музыкальной гармонией и движением планет, а также саму теорию «музыки сфер» подробно
изучал Иоганн Кеплер, опубликовав в 1619 году работу «Harmonices Mundi» (Гармония мира). Более того, в том
же труде Кеплер предположил, что есть связь между орбитами планет и Платоновыми телами, которые в
сакральной геометрии и оккультной химии считаются «кирпичиками» всей материи. Прим. перев.).

Рисунок 11.

Каноническое изображение человеческого тела от Альбрехта Дюрера, как символе выражения всех трех видов
прогрессий и отношений в Единстве.

Рисунок 12.

Различные звуковые частоты заставляют разбросанные случайным образом частицы выстраиваться в
различные геометрические узоры.

Рисунок 13.

Геометрические узоры, формируемые частотными интерференциями электрического луча. Семиконечная
фигура возникает из окружности и возвращается обратно в нее.

Рисунок 14.
Вибрационное изображение базового звука Ом.

Рисунок 15.
В Древнем Египте за эпистемологический базис философии и науки была взята природная способность
откликаться на законы гармонии в звуке и форме. Можно провести аналогию со слепым арфистом, чье
легендарная мудрость происходит не из познания окружающего видимого мира, но из внутреннего знания
метафизических законов, на котором он построен.

Большое количество современных направлений в науке проводят свои изыскания в попытках проверить теории древней
космогонии, в которой указывается вибрационное происхождение всех вещей от Божьего Слова или Космического
звука. Алан Даниэлу (Alain Daniélou) указывал, что мистическая взаимосвязь между вибрацией и формой является
центральной идеей всей духовных учений прошлого:

От атомов до Вселенной каждое движение происходит согласно определенному темпу или ритму или периодичности и может
быть подвержено сравнению с вибрацией, и лучше всего в природе этот эффект выражается с помощью звука. Не все
вибрации доступны нашему уху, но взаимосвязь формы и вибрации может быть понята путем изучения различных частот
слышимых нами звуков. Подобие звуков на разных частотах и форм или объектов идеально лучше всего выразимо
посредством музыки.

Чистые звуки нематериального характера содержат в себе глубочайшую природу вещей, и именно их Кабир называет
«неслышимая музыка». Такие звуки мы можем регистрировать только с помощью специальных приборов, более
чувствительных, чем наши уши. Одной из основных целей психо-ментальной дисциплины, называемой йогой, является
повышение нашей чувствительности, и, в частности, способности распознавать такие звуки.

(Traité de musicologie comparée)

А Джон Вудрофф (John Woodroffe) сопровождая свои переводы с Хинди говорил:

Натуральным именем любой сущности является звук, производимый гармоничным согласным движением сил, действие
которых привело к его созданию. Поэтому говорится, что тот, кто мысленно или физически произносит натуральное имя
сущности, тот дает ей жизнь.

(Garland of Letters)

Желаю Счастья! Сфера сказочных ссылок

Шахерезада

Дата: Понедельник, 2023-04-03, 3:28 PM | Сообщение # 26

Хранитель Ковчега

Группа: Проверенные

Сообщений: 3891

Статус: Offline

Сколько измерений можно выделить в музыкальной гармонии и что это за измерения? Что такое пространство кратностей и как оно помогает понимать и создавать новую музыку? Почему для построения музыкальной гармонии важны простые числа и что такое микрохроматика?

Сказки - жемчуга мира
Книги Семи Морей

MгновениЯ

Дата: Пятница, 2023-04-07, 12:49 PM | Сообщение # 27

Ковчег

Группа: Администраторы

Сообщений: 18316

Статус: Offline

К Теории Земного Монохорда и Теории Струн -
фрагмент статьи даю повторно с целью погружения в возможность интрасферного восприятия многомерности здесь и сейчас - параллельных вселенных. По факту мы в них живем одновременно с линейным временем восприятия трехмерности пространственного мира (но не воспринимаем их ввиду иной мерности Временности).

***
И.М. Капитонов

Что нам известно о космосе и Вселенной.
Существуют ли параллельные миры
(популярная лекция, прочитанная 21 мая 2016 г.
http://nuclphys.sinp.msu.ru/univ/index.html#6.
_______________________________________
d. Последний вариант рассматриваемой нами возможности параллельных вселенных связан с теорией струн – физической теорией, которая в рамках единого подхода пытается объединить все законы природы. Такой единой теории пока не существует и теория струн (более точно, суперструн) – наиболее перспективный теоретический проект. Суперструны – это, пока гипотетические, объекты конечного и очень малого размера (~10–33 см), которые могут испытывать гигантские натяжения и колебаться с различными (и гигантскими) частотами. В этой теории все известные элементарные частицы – электроны, фотоны, кварки (из которых состоят протоны и нейтроны), нейтрино и др. – это различные проявления резонансных колебаний этих струн. Электрон – это один способ резонансных колебаний струны, кварк – другой и так далее. Все свойства каждой элементарной частицы (её заряд, масса и др.) определяются особенностями соответствующего колебания суперструны. Струнная природа частиц должна проявляться при очень высоких, пока недостижимых человеком энергиях (соответственно, видна на очень малых, пока недостижимых расстояниях). Важно то, что размерность пространства-времени в теории суперструн равна 11, из них 10 – пространственных измерений и 1 – временнòе). Мы живём в трёхмерном пространстве. Где же ещё 7 пространственных измерений? Теория утверждает, что эти 7 невидимых (дополнительных) измерений свернуты или сжаты в очень маленькие жгуты (говорят, об их компактификации). Лишь три пространственных измерения протяжённы (развернуты), что позволяет достаточно крупным объектам нашего мира (и нам в том числе) существовать и перемещаться в них. В принципе существует колоссальное разнообразие форм и размеров дополнительных пространственных измерений. Это разнообразие и определяет разнообразие возможных параллельных миров. Стоит чуть-чуть изменить координату какой-либо из дополнительных размерностей, как мы окажемся в другой вселенной, которая практически будет рядом с нами, но не будет нами видна и ощущаться. Это будет в полном смысле параллельная вселенная. Это трудно представить. Обратимся к простейшей аналогии. Пусть мы существуем в пространстве всего с двумя измерениями, из которых одно развёрнуто, а другое сильно сжато. Зафиксируем координату сжатого измерения. Развёрнутое измерение выглядит как тонкая нить, положение на которой определяет координату тела на этой нити. Само тело, если оно имеет достаточные размеры, не способно двигаться в сжатом измерении, а лишь в развёрнутом. Со стороны это будет выглядеть как движение очень тонкого нитеобразного объекта (этакого очень тонкого червячка) по этой нити. Изменим, теперь координату сжатого измерения. Мы окажемся уже в совершенно другом двумерном пространстве. Нить развернутого измерения сдвинулась вдоль сжатого измерения, и эта нить уже не совпадает с предыдущей нитью...

***

Особенности восприятия каждого из нас - ключ к созданию собственной Вселенной, "параллельной", в смысле непересечения с нашей...

Желаю Счастья! Сфера сказочных ссылок

Шахерезада

Дата: Вторник, 2023-05-30, 2:21 PM | Сообщение # 28

Хранитель Ковчега

Группа: Проверенные

Сообщений: 3891

Статус: Offline

Исаак Ньютон, Царлино, И.С.Бах и Пифагорейская Теория

фрагменты книги "Неизвестный Ньютон" Дмитриев И.С.

https://pawet.net/library....2551302

...сэр Исаак стал готовить второе издание «Начал». Многое в нем предполагалось уточнить, изменить и дополнить. Я далее остановлюсь, главным образом, на тех дополнениях, которые Ньютон намеревался включить во второе издание, но затем оставил эту мысль. Эти дополнения вошли в историю под названием «Классические схолии (Classical Scholia)». Они представляют собой комментарии к Предложениям («Пропозициям») IV-IX третьей книги «Начал».

a. Prisca sapientia
В письме Христиану Гюйгенсу от 5 февраля 1691/ 92 г. Фацио де Дюйе сообщал: «Месье Ньютон считает, что ему удалось достаточно ясно показать, будто древние - Пифагор, Платон и другие - располагали всеми доказательствами, кои он предложил относительно истинной системы мира, и кои основываются на том, что тяготение (le Pesanteur) уменьшается обратно пропорционально квадрату расстояния. Он утверждает, что древние авторы сохраняли их знания в величайшей тайне. Но до нас дошли отдельные фрагменты <...>, кои, если их собрать воедино, обнаружат те же мысли, которые рассыпаны в /его/ «Математических началах натуральной философии» [30, с. 193]. В ответном письме Гюйгенс выразил сомнение в том, что Пифагор или Платон имели математическое доказательство эллиптичности планетных орбит, но допустил, что какие-то общие принципы, - к примеру, гелиоцентризм, - вполне могли быть им известны.

В мае 1694 г. Д. Грегори в записях своей беседы с Ньютоном упоминает о том, что последний «говорил о согласии этой философии (т. е. картины мира, представленной в "Началах" - И. Д.) с философией древних, особенно Фалеса. Философия Эпикура и Лукреция истинна сама по себе, но она была ошибочно истолкована древними как атеистическая.

Ясно из названий планет, данных Тотом (египетским Меркурием), что Тот, - а он фактически использовал имена своих предшественников, воспринимая их как богов, - верил в коперниканскую систему» [Ibid, с. 338].

В своих июльских 1694 г. записях Грегори отмечает: «Книгу III ("Начал". - И. Д.) несомненно ждут огромные изменения. Он /Ньютон/ сделал значительные изменения в Гипотезе III [40] <...>. Он покажет, что древнейшая философия находится в согласии с этой его гипотезой, а также, что египтяне и другие /народы/ знали коперниканскую систему, о чем он заключает, исходя из их религии, иероглифики и их изображений богов, а Платон и другие, - Плутарх и Галилей ссылаются на это, - заметили тяготение всех тел ко всем» [Ibid., с. 384].

Действительно, уже в упомянутой «Liber secundus», так и не вошедшей в окончательный текст «Начал», Ньютон утверждал, что древние поклонялись своему божеству в «orbital temples», в центре которых находился «вечный огонь». Такие храмы назывались «prytanea». Египтяне были искусными астрономами, но, с сожалением констатирует лукасианский профессор, они передали свои знания народу, который «больше увлекся (addicted) филологическими занятиями, нежели изучением природы» [117, с. 549-550]. Речь, разумеется, идет о греках. Естественно, при трансляции знания в столь ненадежные руки (точнее, головы) оно было искажено, результатом чего стали аристотелевские представления о твердых небесных сферах и геоцентрическая система мира Птолемея. Истинное же египетское учение, правильно понятое Орфеем и Пифагором (оба были некоторое время в Северной Африке), включает в себя «двоякую философию, как священную, так и вульгарную <...>. Философы изложили священную философию с помощью символов и загадок, но поскольку проповедники передали открыто лишь вульгарную версию и в широко распространенном стиле <...>, /священная/ философия процветала лишь в Египте; она была основана на знании звезд. Это видно из ежегодной процессии жрецов, которая устраивалась в честь этого знания <...>. Процессия замыкалась Верховным жрецом и Смотрителем священных предметов, сведущим в теологии и в религиозных церемониях. Связывая свое знание звездного неба и мира с теологией и отдавая этому знанию пальму первенства, египтяне намекали на то, что их теология обращена к звездам» [168].

Однако египтяне «скрыли те тайны, понять которые толпа (common herd) была неспособна, под покровом религиозных ритуалов и иероглифических символов». Орфей усвоил истинную египетскую теологию, а Пифагор постиг «значения символов и чисел», а также «искусство мистического рассуждения и аллегорического разговора о числах и символах». Среди своих учеников Пифагор «распространял коперниканскую астрономию». То же делал и древнеримский царь Нума Помпилий (ок. 700 до н. э.) [117, с. 549]...
...

В рассуждениях древних авторов мысль о гармонии мира, а точнее, пифагорейско-платоническая идея божественного упорядочения и гармонизации изначально хаотического материального универсума, была, пожалуй, наиболее близка Ньютону. О понимании английским ученым пифагорейской традиции следует сказать особо.

По наблюдению Доббс [136, с. 195-196], ньютонов взгляд на учения Пифагора и Платона во многом созвучен их толкованию ранними христианскими апологетами: Филоном Александрийским (ок. 25 г. до н. э.- ок. 50 г. н. э.), Юстином Мучеником (II в), Татианом (род. ок. 120 г.), Климентом Александрийским (ок. 150-ок. 215 г.) и др. [43]

Так, по мысли Филона, красота и разумность мирового порядка, единство мира должны возбуждать идею о едином творце этой красоты, гармонии и порядка. «Таинственный ветхозаветный бог приоткрывал свою сущность в "логических" манифестациях. В свою очередь, само рациональное, логическое приобретало черты божественного и богооткровенного. Согласно Филону, Библия и греческая философия не противоречат друг другу и именно потому, что как та, так и другая порождены Логосом: первая божественным Логосом, открывшим себя пророкам непосредственно, вторая - Логосом, отраженным в человеческом разуме и в мире. Мудрость Моисея, Пифагора и Платона имеет один и тот же источник. <...> (De mut. 19-21). Самораскрытие "естественного" Логоса неизбежно приводит к исходному библейскому монотеизму. Однако Пифагор и Платон, по мнению Филона (а также других раннехристианских апологетов, например, Юстина. - И. Д.), ближе других подошли к монотеизму не только благодаря "логической" одаренности и проницательности, но и благодаря прямому заимствованию из Библии» [17, с. 52]. Если верить Филону, Юстину и Татиану, то греки «похитили» философию у иудеев, не добавив к ней ничего, кроме ошибок, искажений и заблуждений (см., например, речь Татиана «Adversus graecos» [181, с. 369-404]). Типичная цепочка заимствований, выстраиваемая грекоязычными апологетами II в., выглядит так: стоики и Аристотель заимствовали свои идеи у Платона, Платон - у Сократа, Сократ - у Пифагора, Пифагор - у брахманов, магов, египтян и иудеев, а те - от самого Бога. А поскольку трансляция идей неизбежно сопровождалась их порчей, то критерием глубины и истинности доктрины часто служила ее древность. Поэтому пифагореец Нумений Апамейский (втор. пол. II в.), которому принадлежит известное выражение о Платоне: «Моисей, говорящий по-аттически», ставил, однако, Пифагора выше Платона.

Ньютон в целом разделял подобные взгляды, связывая их с неоплатоническими представлениями, воспринятыми затем христианскими мыслителями, о вездесущности божества (Бог как пронизывающий всю Вселенную всепроникающий дух) [44] и о Боге как создателе (строителе) и упорядочивающем начале Космоса. Сердцевиной пифагоро-платонистического учения о гармонии мира было учение о числе. «У пифагорейцев, а за ними, можно сказать, и во всей античности, реальная действительность на всех ступенях своего развития всегда мыслилась числовым образом устроенной, так что без числовой структуры античный философ вообще не мыслил ничего существующего, будь то материальное, будь то душевное или умственное, будь то абсолютное первоединство, будь то неживая вещь, будь то человек, будь то сам Бог. <...>. Эта числовая теория, аритмология, была для античности самым настоящим априоризмом, под который подгонялось всякое позитивно-реальное и даже экспериментальное наблюдение» [183, с. 133].

Этот аритмологический априоризм лежал в основе пифагорейского учения о музыкальной гармонии.

b. Harmonice Mundi
Как известно, отношение тонов в интервале можно выразить численно, т. е. в виде отношения чисел. Сделать это можно двояко: либо через отношение длин струн, либо через отношение частот колебаний. Древние, естественно, шли по первому пути. При этом в Античности сложилось два метода оценки качества звучания: пифагорейский метод основывался на оценке числовых отношений; метод, характерный для школы «гармоников» ученика Аристотеля Аристоксена из Тарента (IV в до н. э.), основывался на субъективных ощущениях.

Если обратиться к пифагорейской акустической традиции, то в ее рамках музыкальная наука оперировала тем же аппаратом, что арифметика, геометрия и астрономия. На это обращали внимание и в после-пифагорейские времена. Платон утверждал, что музыка и астрономия - родные сестры (Государство, 7, 530). Аристотель писал в «Метафизике» (XIV, 3, 1090а), что числа имеют отношение к гармонии звуков и к строению неба. Короче, музыка понималась как математическая дисциплина. «Ту величину, которая существует сама по себе, - утверждал Боэций, - полностью изучает арифметика, а ту, которая /сопоставляется/ с какой-либо /другой величиной/ <...> осваивают по соразмерностям гармонии. Геометрия обещает знакомство с неподвижной величиной, а знание подвижной /величины/ присваивает наука об астрономическом учении» (цит. по [184, с. 28]).

Однако, сколь ни важны числовые соответствия, полностью отказаться от слуховых оценок невозможно, поэтому необходимо было «хотя бы частично согласовать математические формы фиксации интервалики со слуховыми ощущениями» [185, с. 156]. Согласно чувственным критериям, интервалы были разделены на консонансные и диссонансные. Греческое ухо со времен Пифагора в качестве консонансных интервалов воспринимало кварту, квинту и октаву (иногда добавляли дуодециму = октава + квинта и двойную октаву).

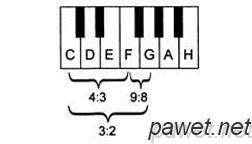
Как именно устанавливались числовые пропорции для этих интервалов - вопрос весьма запутанный. Широкое распространение получил рассказ о том, как Пифагор, проходя мимо кузницы, заметил, что четыре разных молота, ударяясь о железо, издавали тоны, равные по отношению к самому низкому тону, кварте, квинте и октаве. Пифагор, гласит далее легенда, взвесил эти молоты, и оказалось, что их веса относятся между собой как 6:8:9:12. Отношение 12:6, т. е. 2:1, отвечало октаве; отношение 9:6 (или 3:2) - квинте, а 8:6 (или 4:3) - кварте. Есть иной вариант этого исторического анекдота, согласно которому Пифагор натягивал одинаковые по толщине и длине струны, подвешивая к ним грузы, отношение весов которых составляло 6:8:9:12. Но высоты тонов при этом определяются отношением квадратов весов грузов, т. е., чтобы получить звучания кварты, квинты и октавы, веса грузов должны быть в отношении 2 2:3 2:4 2 , а не 4:3:2 (рис. 6).

Пожалуй, наиболее точные результаты могли быть получены в опытах с разделением струны на отрезки. Если, к примеру, на монохорде (инструменте с одной струной, натянутой на линейку с размеченными делениями - всего 12 делений) сначала заставить звучать всю струну, а затем, зажав ее посередине, - половину струны, то эта половина будет звучать на октаву выше, чем вся струна. Отношению 3 : 2 (сначала звучит вся струна, 12 делений, а затем 2/3 ее, 8 делений) отвечает квинта, а отношению Рис. 6. Пифагор. Иллюстрация из книги Ф. Гафурио «Theorica Musice» (1492).4 : 3 (эпитрит, когда сначала звучит вся струна, 12 делений, затем 3/4 струны, 9 делений) - кварта. Отношению 4:1 - двойная октава, а 3 : 1 - дуодецима (= октава + квинта) [183, с. 136].

Сказки - жемчуга мира
Книги Семи Морей

Сообщение отредактировал Шахерезада - Вторник, 2023-05-30, 2:25 PM

Шахерезада

Дата: Вторник, 2023-05-30, 2:21 PM | Сообщение # 29

Хранитель Ковчега

Группа: Проверенные

Сообщений: 3891

Статус: Offline

Было замечено, что отношение, отвечающее дуодециме, получается перемножением отношений, характерных для октавы и квинты: [45]

3 : 1 = (2 : 1)-(3 : 2).

Далее,

квинта + кварта = октава и в то же время

(3 : 2) • (4 : 3) « 2 : 1 или в логарифмической форме:

log 2(3/2) + log 2 (4/3) = log 2(2/l)

Таким образом, сложению смежных интервалов отвечает умножение соответствующих им числовых пропорций. Вычитанию интервалов, имеющих общий нижний тон, отвечает деление соответствующих числовых отношений. Например: квинта - кварта = тон (3:2): (4 : 3) = (9 : 8) (эпогдоус)

См. рис. 7.

Отношения чисел, отвечающие трем основным консонансным интервалам, выражаются, в итоге, с помощью четырех первых чисел натурального ряда: 1,2,3 и 4 (так называемая «пифагорейская тетракида»).

Рис. 7. Числовые отношения для различных музыкальных интервалов.
Все многообразие созвучий, включая и консонансные, можно было выразить числовыми отношениями трех типов:

n : 1 (2 : 1; 3 : 1 и т. д.) - «многократные» («multiplex»);

(n+l)/n (4 : 3; 3 : 2; 9 : 8 и т. д.) - «сверхчастные» («superparticularis »)

и остальные, которые в Античности признавались негодными для фиксации музыкальными инструментами.

В терминах отношений длин струн консонансы выражались (в пределах одной октавы) следующим числовым отношением: 12 : 9 : 8 : 6. Крайние члены этого отношения использовались для построения средних величин, которые выражались «внутренними» членами приведенного отношения:

среднее арифметическое: (12 + 6)/2 = 9 среднее геометрическое: √12 • 6 = √9 • 8 среднее гармоническое: 2 • (12 • 6)/ (12 + 6) = 8

Эти выражения, согласно пифагорейской традиции, давали ключ к структуре Вселенной.

Аристоксен, следуя Архиту Тарентскому, ученику Платона, предложил более удобное, чем у пифагорейцев, деление гаммы. Он разделил кварту на 60 равных частей, из которых первые 24 и вторые 24 части образовывали по одной большой секунде, а остальные 12 частей - малую секунду. Если провести подобное деление по всей октаве, то получится система 12-ти полутоновых ступеней. Но такая система казалась искусственной и распространения не получила.

Пифагорейская гармония - теоретико-числовая и акустическая - имела также и геометрическую реализацию. Единица понималась при этом как точка, двойка - как отрезок прямой, соединяющий две точки, тройка - правильный треугольник, четверка - тетраэдр (т. е. точка=»линия =»плоскость=»пространственный образ). Отсюда один шаг до космологической интерпретации музыкальной гармонии.

Действительно, космический планетный семичлен (сферы Луны, Солнца, Меркурия, Венеры, Марса, Юпитера и Сатурна) считался в древности «воплощением тех отношений, которые царят в октаве, так что среди этих семи космических сфер находили свои тоны, свои кварты, свои квинты, свои октавы и еще другие, более сложные пропорции» [183, с. 144].

По античным представлениям, всякое движение порождает звук. Это утверждение понималось как универсальный мировой закон, которому подчиняются также и планетные движения. Звучание, обусловленное перемещением огромных космических тел, подчинено законам гармонии. Отсюда термин «гармония сфер». «Все тела, - писал Никомах в "Руководстве по гармонике", - рассекающие со свистом что-то податливое, очень легко приводимое в движение, обязательно создают /своей/ величиной и местом звучания отличающиеся между собой звуки - либо в зависимости от своих масс, либо в зависимости от своих скоростей, либо периодов (более подвижных или, наоборот, более спокойных), в которых осуществляется вращение каждого /небесного тела/» (цит. по [184, с. 290].

Кассиодор спустя четыре столетия придал языческой идее «гармонии сфер» иной, христианский смысл: «...само небо, вращаясь, подчиняется сладостной гармонии, и, чтобы кратко выразить суть /небесной музыки, нужно сказать/: все, что осуществляется по велению Творца в небесных и земных делах, не осуществляется без того, что предусмотрела эта наука /то есть, музыка/» (цит. по [Ibid.]).

Идея подобия макро- и микрокосма подсказывала мысль о единстве небесной и земной музыки. Земная гармония - это, по выражению Боэция, «прообраз небесного звукоряда».

Согласно же Платону, космические сферы не только настроены музыкально в определенном отношении, но и наделены притягательной силой («Государство» X, 617в.).

В уцелевшем фрагменте последней книги трактата Цицерона «О государстве» (IV, 17) можно встретить звуко-планетное соответствие, которое в современных обозначениях имеет следующий вид:

ля - Луна

си - Меркурий

до - Венера

ре - Солнце

ми - Марс

фа - Юпитер

соль - Сатурн

Ля - небесный свод.

Упомянутый выше Никомах из Герасы (II в.) дает несколько иной звуко-планетный ряд:

ми - Сатурн

фа - Юпитер соль - Марс

Ля - Солнце

До - Венера

Ре - Луна [Ibid., с. 291].

Комментируя эти соответствия, Е. В. Герцман отмечает следующие обстоятельства: «Цицерон излагает октохорд, а Никомах - гептахорд. Эти два варианта отражают два исторических этапа развития музыкальной системы. Когда более древний гептахорд был заменен на октохорд, то понадобилось и еще одно небесное тело. И здесь, как видно, возникло затруднение. Ведь античная наука знала только семь планет. Поэтому, когда в теории музыки стал фигурировать октохорд, появилась сложная ситуация: для восьмого звука потребовалась еще одна планета. И выход был найден: вместо планеты к новому звуку октохордной системы был "приписан" небесный свод, то есть сфера неподвижных звезд, которая, по бытовавшим в античности воззрениям, обращалась вокруг Земли за одни сутки» [Ibid.]. При этом в одной системе нижнему звуку отвечает Луна, а верхнему - Сатурн, тогда как в другой - наоборот. «Представляется, что точка отсчета для планет здесь не играла никакой роли. <...> Главным условием правдоподобности (указанных рядов. - И. Д.) было лишь сохранение порядка небесных тел: от Луны к Сатурну и обратно» [Ibid., с. 292].

Но почему же никто не слышал этой «небесной симфонии»? Одни мыслители полагали, что эта музыка сопровождает человека изначально, с момента его появления на свет, и потому люди настолько к ней привыкли, что не реагируют на нее (см. Аристотель, «О небе», II 9, 290 в 25). Другие же утверждали, что столь мощное звучание ограниченный человеческий слух не воспринимает (Цицерон, «О государстве», VI, 5, 18-19). Оригинального мнения на этот счет придерживался И. Кеплер. Он полагал, что движение по круговым орбитам порождает монотонное звучание, характерное для древнегреческой музыки, тогда как движение по эллиптическим орбитам порождает полифоническую музыку, слышать которую, однако, дано лишь Творцу.

До эпохи Ренессанса пифагорейская школа была принята как идеальная для настройки большинства существовавших тогда музыкальных инструментов. Поскольку сочинения многих античных авторов до этого времени либо вовсе не дошли, либо были известны по отдельным фрагментам, то пользовались трактатами Боэция «Наставления к музыке» и «Sectio canonis» Эвклида. В частности, эти сочинения служили стандартными учебниками и в Оксфорде, и в Кэмбридже практически до XVIII столетия [186, с. 76-78].

Однако пифагорейская шкала имела существенные недостатки, которые с развитием музыкального искусства (расширением звукового диапазона, введением многоголосия и т. д.) все ощутимее давали о себе знать. Суть проблемы состояла в следующем (проиллюстрирую на современной фортепьянной клавиатуре, состоящей из семи октав или двенадцати «совершенных квинт»). Если идти от «до» нижней октавы до «си» седьмой октавы сначала по октавам, а затем по квинтам, то, казалось бы, мы в обоих случаях должны прийти в одну и ту же «точку» (ноту). Но по пифагорейской теории так не получается, поскольку: (2 : 1) 7< (3 : 2) 12.

Т. е. двенадцатая чистая квинта была математически больше, чем седьмая октава, на величину, которая получила название пифагорейская комма.

Были и иные несоответствия. Так, например, большая терция, которая на слух воспринималась как консонанс, математически относилась к диссонансам:

большая терция = тон + тон - (9 : 8) • (9 : 8) = 81/64.

Пока музыка была гомофонной и преимущественно вокальной (церковное пение), где голоса двигались строго параллельно, с интервалом в октаву, квинту или кварту, указанных трудностей можно было и не замечать. Но когда (примерно с XV в.) появилась полифония и стали использовать терции и сексты, надо было менять шкалу.

В 1558 г. итальянский музыкант и теоретик музыки Джозеффо Царлино предложил следующее усовершенствование. Он разбил чистую квинту на два смежных интервала - большая терция + малая терция, - считая обе терции консонансами, т. е. им должно отвечать числовое отношение типа (п+1)/п. Тогда:

квинта - 3/2 = {(n+l)/n}-{(n+2)/(n+l)}, откуда п = 4.

Таким образом получалось, что малой терции должно отвечать отношение 6/5, а большой - 5/4. Но тогда возникли новые проблемы, в частности, проблема тона:

а) большая секста = чистая квинта + тон,

т. е. тон - 5/3 : 3/2 = 10/9, а не 9/8, как у Пифагора.

б) большая терция = тон + тон,

т. е. 5/4 = а • а, откуда а = V5/2 , что неприемлемо.

Поэтому Царлино выбрал другое представление: 5/4 = (10/9)-(9/8),

т. е. получалось, что для тона существуют два отношения: по Пифагору (9/8) и по Царлино (10/9). Разница между ними (синтоническая комма) небольшая (81/80), но она сказывалась при настройке музыкальных инструментов.

Иными словами, шкала Царлино оказалась неустойчивой, но, поскольку коммы были очень малы и терпимы для слуха, она получила широкое распространение. Однако потребность в ее усовершенствовании оставалась (см. подробнее [187]), а точнее, оставалась потребность в нахождении разумного компромисса между ratio и sensus, или, если воспользоваться теоретико-музыкальной терминологией, нужен был temperamentum, хорошо темперированный строй (темперация - выравнивание интервальных соотношений между ступенями звукоряда). Кончилось тем, что И. С. Бах, старший современник Ньютона, предложил немного уменьшить величину каждой квинты так, чтобы выполнялось условие: 7 октав = 12 акустически чистым уменьшенным квинтам, и все тона и полутона стали бы равными. Такой строй получил название равномерно темперированного. [46]

и далее по ссылке выше

Сказки - жемчуга мира
Книги Семи Морей

MгновениЯ

Дата: Понедельник, 2023-07-03, 11:18 PM | Сообщение # 30

Ковчег

Группа: Администраторы

Сообщений: 18316

Статус: Offline

Объединяющая научная теория - Теория Всего

Желаю Счастья! Сфера сказочных ссылок

MгновениЯ

Дата: Пятница, 2023-09-22, 9:21 PM | Сообщение # 31

Ковчег

Группа: Администраторы

Сообщений: 18316

Статус: Offline

В Греции существовали особые храмы, куда приходили люди, страдающие от бо¬лезней. Главным орудием исцеления в этих храмах была музыка: приводя в гармонию тело и дух человека, она за¬ставляла недуги отступить. Одним из самых выдающихся мыслителей Греции, чьё учение не утратило актуальности и до сей поры, был Пифагор. Этот философ, живший в VI в. до н.э., известен нам как великий посвящённый, выдающийся философ, основоположник математики, музыкальных законов, геометрии и этики. Он первым из учёных установил соотношение между музыкальными интервалами.

Для Пифагора и его учеников понятие «музыка сфер» было не просто метафорой. Великий философ на самом деле обладал способностью слышать, как плывут планеты по своим небесным орбитам. Взаимосвязь слышимого звука и звуков небесных тел на протяжении многих веков волновала умы многих мыслителей. И лишь недавно, используя математические принципы, основанные на вычислении орбитальной скорости планет, учёным удалось соотнести определенные звуки с определенными планетами. И вот удивительный результат: эти звуки оказались гармонически связанными!

В наше время на роликах Ютуба уже можно услышать их вариации, гармоничные звуки планет!
Гармоники порождаются любой формой вибрации. Возможности человека слышать звук далеко не беспредельны. Наше ухо способно воспринимать колебания лишь от 16 до 25 000 Гц, но за пределами этого ограниченного диапазона существуют неисчислимые множества звуковых волн, которые мы не слышим.
Вселенная, по сути, состоит из вибраций, каждый заключённый в ней объект — от электрона, вращающегося вокруг ядра атома, до планеты, вращающейся вокруг звезды, — обладает собственным основным тоном и обертонами.

Желаю Счастья! Сфера сказочных ссылок

Белоснежка

Дата: Среда, 2023-12-20, 12:12 PM | Сообщение # 32

Хранитель Ковчега

Группа: Модераторы

Сообщений: 6041

Статус: Offline

Пифагорейское правило:
Избегай всякую хитрость, отсекай огнем, железом и любым орудием от тела
болезнь, от души — невежество, от утробы — роскошество, от города —
смуту, от семьи — ссору, от всего, что есть, — неумеренность»

ЯМВЛИХ

фрагмент

ЖИЗНЬ ПИФАГОРА

Глава IX

45. Когда юноши рассказали своим отцам о том, что он говорил, совет тысячи пригласил Пифагора на заседание. Сначала они похвалили его за то, что он сказал их сыновьям, и попросили его, если он хотел сказать что-нибудь полезное для кротонцев, сделать это перед высшими должностными лицами города. Он сначала посоветовал им воздвигнуть храм Музам, дабы они охраняли царящее гражданское согласие, ведь эти богини одинаково называются музами, предание всегда говорит о них вместе, и они особенно радуются общим для всех них почестям. Вообще хоровод Муз всегда один и тот же, охватывающий звук, гармонию, ритм — все, что ведет к согласию. Он показал, что власть Муз распространяется не только на прекраснейшие учения, но также и на созвучие и гармонию существующих вещей.

46. Затем он сказал должностным лицам, что им следует понять, что они владеют своим отечеством как общим достоянием, вверенным им большинством граждан, поэтому управлять им следует так, как будто они собираются передать обязательства потомкам. Так несомненно и будет, если они будут справедливы со всеми гражданами и никому не дадут больше, чем по справедливости. Ведь люди, понимая, что всякое место в мире нуждается в справедливости, создали миф о том, что одно и то же место занимает при Зевсе — Фемида, при Плутоне — Дике46, а в городах — закон, чтобы тот, кто поступает несправедливо по отношению к установлениям, оказывался тем самым нарушителем всего миропорядка.

47. Члены совета не должны злоупотреблять именами богов в клятве, но следует употреблять такие слова, которые и без клятвы вызывают доверие47. Домашнее хозяйство им следует вести так, чтобы можно было ссылаться на это в их политике. К своим детям им следует относиться благожелательно, ибо это единственное общее качество всех живых существ. И с женой, разделяющей с мужем жизнь, следует общаться исходя из того соображения, что как договоры с другими людьми бывают записаны или высечены на камне, так договоры с женщинами состоят в детях. Следует стараться, чтобы дети любили нас не из-за родства, за которое они не ответственны, а по собственной воле, ведь это благодеяние добровольно.

48. Они должны заботиться также и вот о чем: чтобы жить лишь с законными женами и чтобы женщины не имели внебрачного потомства из-за пренебрежения и порочности своих мужей. А также им следует считать, что жена как просительница перед богами взята с симпатией от очага и введена в новый дом48. Дисциплиной и благоразумием они должны стать примером для домочадцев и сограждан и должны заботиться о том, чтобы никто ни в чем не погрешил, так, чтобы не злоумышленники скрывались из страха перед наказанием, но чтобы люди, руководствуясь совестью в достойном образе жизни, сами стремились к справедливости.

49. Он также советовал им оставить нерадивость в делах, ибо нет ничего лучше, чем мера в каждом деле. Самой большой несправедливостью он считал разлучать детей и родителей друг с другом. Самым могущественным он считал того, кто сам может предвидеть, что ему полезно, вторым — того, кто на примере случившегося с другим понял, что полезно ему самому, а самым плохим — того, кто на собственном опыте испытав неудачи, выбирает правильное решение. Он сказал, что не ошибется, если уподобит желающих снискать почести победителям в беге, ведь они не делают зла соперникам, но стремятся добиться победы сами по себе. Участвующим в политической жизни не следует выражать недовольство противниками, но, выслушивая, извлекать пользу. Он призвал всех, кто дорожит добрым именем, быть такими, какими они хотят казаться в глазах других, ведь для городского совета нет ничего столь священного, как похвальная речь, потому что совет нужен только людям, а похвала больше нужна богам.

50. Потом он рассказал всем, что, по преданию, их город основал Геракл, когда гнал стадо быков через Италию и ему нанес обиду Лакиний Геракл, приняв ночью по ошибке Кротона, помогавшего ему, за одного из врагов, убил его. После этого на его могиле он обещал основать город и назвать его тем же именем, а сам Геракл причастен бессмертию. Пифагор сказал, что они должны вести дела справедливо, воздавая Гераклу благодарностью за благодеяние. Они же, выслушав его, основали храм Муз и отпустили наложниц, держать которых было у них в обычае, а также попросили Пифагора побеседовать отдельно с мальчиками в храме Аполлона, а с женщинами — в храме Геры.

Привет с Волшебного острова Эхо!
остров

Город Мастеров

Галактический Университет

В главный зал Библиотеки Ковчега

Страница 2 из 2 « 1 2
Модератор форума: Танец